A circle is a simple closed shape. The mathematical definition of circle is it is a set of all points in a plane which are at a constant given distance (radius) from a given point (center). Explained using conic sections, a circle is a conic section obtained by the intersection of a cone with a plane perpendicular to the cones symmetry axis. Circle is a two- dimensional figure having no edge and no vertex. So as any regular two- dimensional closed figure, it has two main properties i.e. it has a perimeter and an area.
Here we will be looking at how to calculate the perimeter or the circumference of the circle. Lets first look through the basic terminology.
- Perimeter or circumference is the continuous line forming the boundary of closed geometrical figure
- Area is the quantity that expresses the extent of a two- dimensional figure or shape in the plane.
- The center of circle is a point which is equidistant from the points on the edge of the circle.
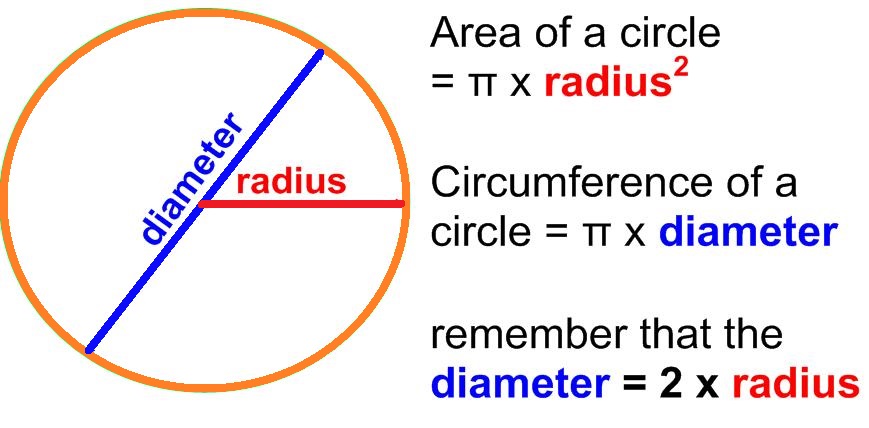
- The radius of a circle is the distance from the center point to the point on the circle. Since, circle has radial symmetry, the distance is same of a circle.
- The straight line passing from one side to the other through the center of the circle is called the diameter.
- The number pi or ? is a mathematical constant used to calculate the circumference and the area of the circle. Being an irrational number, ? cannot be expressed as an exact numerical form but it is usually generalized as 3.14 or 22/7 for calculation purposes.
Before the formula were created, there were other ways to calculate the circumference of the circle.
For instance, a string was used to go along the continuous boundary of the circle and it was straighten to check the perimeter it covers.
Here, we will talk about three formulas of calculating the circumference of a circle
When the radius is given-
The formula used when the radius of a circle is given is:
- C=2?r
Here, C is the circumference and r is the radius given.
Lets learn this using an example-
- Calculate the circumference of circle with radius 14cm
Solution – here, the radius given is, r = 14 cm
- C=2?r
- C= 2?14
- C= 2(22/7)(14) or 2(3.14)(14)
- C= 88 cm
Hence, the circumference of the circle is 88 cm.
When the diameter is given-
The formula used when the diameter of a circle is given is-
- C=?d
Here, C is the circumference of the circle and d is the given diameter of the circle.
Lets learn this using simple problem-
- Calculate the circumference of the circle of diameter 14 cm.
Solution- here, diameter given is, d = 14 cm
- C=?d
- C=?14
- C= 22/7(14) or 3.14(14)
- C= 44 cm
Hence, the circumference of the circle is 44 cm.
When the area of the circle is given-
This formula might look a bit complicated, but it isnt.The formula used when the area of the circle is given is-
- C= 2 ? ? A
Here, C is the circumference of the circle and A is the given area of the circle.
Lets learn this using simple problem-
- Calculate the circumference of the circle of area 14 cm
Solution- here, area given is, A = 14 cm
- C= 2 ? ? A
- C= 2 ? ? (14)
- C= 2 ? (22/7)(14) or C= 2 ? (3.14)(14)
- C= 13.26 cm
Hence, the circumference of the circle is 13.26 cm




































